Análisis estadístico para pruebas de diferenciación de dos muestras.

( Puede aplicarse en pruebas pareadas, dúo-trío y triangular.)

El objetivo principal de estas pruebas es determinar si existen diferencias entre las dos muestras que se comparan.

En general los métodos estadísticos que se aplican en estos casos permiten estimar a partir de los resultados experimentales, parámetros con los cuales se calcula un estadígrafo dado, el cual mediante la ley de probabilidades puede comprobarse si coincide o no con la ley teórica correspondiente.

Los resultados se expresan refiriéndolos siempre a un nivel de significación previamente elegido, y en su cálculo se tiene en cuenta la posibilidad de que las respuestas emitidas por los jueces sean producto del azar.

• Prueba de Ji cuadrado (χ2).

La prueba ji cuadrado se utiliza para probar de acuerdo con una cierta hipótesis en que grado una distribución de frecuencia observada se compara con una distribución esperada; permite comparar dos muestras y saber si son diferentes significativamente o no. Puede aplicarse en pruebas pareadas, dúo-trío y triangular.

El procedimiento de la prueba es el siguiente:

• Calcular χ2 experimental según:

Xi = Número de respuestas correctas

n = Total de ensayos realizados

p = Probabilidad máxima de respuestas debidas al azar.

0,5 = Factor de corrección, se aplica sólo para 1gl en el cual los resultados se consignan como aciertos o fallos.

• Se compara el valor de χ2 experimental con el valor de χ2 tabulado en la tabla correspondiente, según los grados de libertad (gl=1) y el nivel de probabilidad establecido.

• Si χ2 exp. ≤ χ2 tab. Se acepta H0: No hay diferencia entre las muestras.

χ2exp. > χ2 tab. Se rechaza H0: Si hay diferencia entre las muestras

Ejemplo:

Un equipo de 10 jueces adiestrados evaluó por triplicado dos dulces elaborados con diferentes por ciento de sustitución de harina de trigo por salvado de arroz.

Se desea conocer si existe diferencia en los productos para un 95% de confianza, empleando para ello una prueba pareada.

Al aplicar la prueba se obtuvo que de los 30 juicios, sólo 21 fueron correctos. Es decir 21 de

los jueces participantes consideraron las muestras diferentes.

Datos obtenidos:

n =30 (total de juicios)

Xi =21 (juicios correctos)

p =1/2 =0,5 (probabilidad del azar)

Recuerde que si la prueba es triangular p=1/3; en la prueba pareada hay que tener en cuenta si es de una cola o dos colas.

Procesamiento de los resultados

Como χexp 2 > χ tab 2 Existe diferencia significativa entre las muestras para un nivel de significación de 0,05 El método más fácil y simple para conocer la significación de los resultados que se obtienen en las pruebas donde se analizan dos muestras (pareada dúo-trío, triangular) es a través de la comparación de los datos obtenidos de manera experimental con los valores que aparecen en las tablas creadas a tal efecto. Dichas tablas ofrecen el número mínimo de juicios concordantes necesarios en función del número total de pruebas realizadas, para rechazar la hipótesis nula.

Análisis estadístico aplicado a la prueba de ordenamiento

El procedimiento que se establece para analizar los datos de la prueba de ordenamiento por rangos se basa en el Test de Fridman. Debe tenerse en cuenta si la prueba se diseña como de dos colas o una cola. Esto es si se comparan todos los tratamientos entre si, o si una de las muestras se establece como referencia a comparar con las restantes, bien porque se desee probar que es superior o inferior dentro de un grupo de muestras (diferencia direccional) o simplemente determinar si es diferente al resto de las muestras (diferencia no direccional).

El procedimiento a seguir es el siguiente.

1. Asignar puntuaciones a las muestras según el orden que se le haya dado

2. Obtener suma total de puntos para cada tratamiento, después que han sido

ordenados.

3. Calcular el valor de Ji cuadrado experimental, según la formula siguiente:

Donde:

n= número de juicios totales.

K= número de tratamientos.

Ri= suma de puntos totales por muestra.

4. Buscar χ2 tab en la tabla correspondiente para un nivel de significación elegido y K-1 grados de libertad

5. Comparar X2 exp con X2 tab.

6. Si χ2exp ≤ χ2 tab " No hay diferencia significativa entre las muestras para un nivel de significación dado.

Si χ2 exp > χ2 tab " Hay diferencia entre las muestras para un determinado nivel de significación.

7. Si no hay diferencia entre las muestras se concluye el análisis, de lo contrario es necesario precisar cuales son los tratamientos diferentes, de ahí que sea necesario calcular la diferencia mínima significativa (DMS)

Donde:

Q= Valor tabulado según K y nivel de significación establecido

n= número de juicios totales.

K= número de tratamientos.

8. Se determina el valor modular de la diferencia de puntuación total de los tratamientos, realizando todas las combinaciones posibles y se compara con el valor de DMS calculado.

9. Si /Ri1-Ri2/>DMS " Hay diferencia significativa para el valor de alfa elegido.

Si /Ri1- Ri2/ ≤ DMS " No hay diferencia significativa para el valor de alfa elegido.

Ejemplo:

Se evaluaron cuatro jugos de frutas y se ordenaron en orden creciente según su sabor dulce. Los códigos de las muestras son: 128, 056,721 y 980.

Se obtuvieron los datos que se presentan a continuación.

Datos ordenados.

ANALISIS DE VARIANZA APLICADO A LAS PRUEBAS DE ESTIMACION

DE MAGNITUD.

Cuando se necesita establecer un criterio psicológico en relación a las diferencias proporcionales que puedan indicar la intensidad de un estímulo específico de dos o más muestras se utiliza la prueba de estimación de magnitud y los resultados se procesan generalmente a través de análisis de varianza, una vez normalizados los datos.

El procedimiento que se emplea es el siguiente:

1. Hallar la media geométrica (MG) a la respuesta de los jueces.

2. Calcular una constante (K) para cada juez.(cociente de dividir 10/MG)

3. Normalizar los datos. (Respuesta del juez)( K)

4. Obtener el logaritmo de los datos normalizados.

5. Realizar el análisis de varianza (ANOVA).

6. Determinar la Diferencia Mínima Significativa. (Sólo si se concluye al realizar el ANOVA que existe diferencia significativa entre las muestras).

Donde.

t : Valor de t student tabulado para el nivel de significación prefijado (α) y los grados de libertad del error en el ANOVA. (Tabla 3)

cme : Cuadrado medio del error en el ANOVA

Ejemplo:

Una comisión de evaluación sensorial compuesta por 5 jueces analizó tres muestras diferentes de puré de tomate, con el objetivo de conocer si existía diferencia apreciable en el color de las mismas. Se empleo la prueba de estimación de magnitud con modulo fijo 10.

· Procesamiento de resultados

· Calculo de la media geométrica para cada juez

• CALCULO DE K

• NORMALIZACIÓN DE DATOS

Cálculo del logaritmo de los datos normalizados.

Juez 1; muestra 125 = Log 5.50=0.7404

Juez 1; muestra 008 = Log 11.00=1.0414

. .

. .

Juez 5; muestra 497= Log 20.01=1.3012.

• ANALISIS DE VARIANZA DE CLASIFICACIÓN SIMPLE

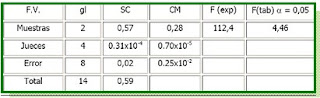
Como F(exp.)> F(tab.), existe diferencia significativa entre las muestras para p<0.05.

• CALCULO DE LAS MEDIAS MUESTRALES

COMPARACIÓN DE LA DIFERENCIA MODULAR DE LAS MEDIAS CON EL VALOR DE DMS.

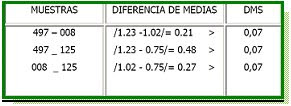
Se concluye que existe diferencia proporcional significativa en el color de las tres muestras analizadas para un 95% de confianza.

PRUEBA DE INTENSIDAD

Los resultados se analizan a partir de las curvas medias construidas para cada muestra con los valores obtenidos de cada juez (ver Fig. 1). La gráfica resultante permite obtener los parámetros siguientes:

• Intensidad máxima del estímulo (I máx.).

• Tiempo para alcanzar la máxima intensidad (Tmáx).

• Duración de intensidad máxima (D máx.).

• Tiempo desde que se alcanza la intensidad máxima hasta que se extingue la intensidad(Tmáx-ext).

• Duración total del estímulo (D total).

• Tiempo de extinción (T ext).

• Área bajo la curva.

PRUEBA DE PERFIL DE SABOR

Para calificar la amplitud inicialmente se utilizaban los términos y escalas que se describen a continuación:

)( muy baja

1 baja

2 media

3 alta

Como modificación a lo anterior se recomienda no emplear el término muy baja y utilizar sólo las variantes de amplitud siguientes:

1 baja

2 media

3 alta

Los resultados que se obtienen al efectuar la prueba se procesan estadísticamente y además se representan gráficamente mediante líneas que representan los términos descritos.

Dichas líneas se colocan simétricamente separadas y la extensión de cada una se corresponde con la escala de intensidad utilizada.

Una gráfica puede representar más de una muestras, siempre que las líneas descriptoras se identifiquen adecuadamente para cada muestra y no origine confusiones.

Representación gráfica de un perfil de sabor.

Olor a cola

PRUEBA DE ANALISIS CUANTIATIVO DESCRIPTIVO

Para procesar los resultados y obtener los valores dados para cada atributo se mide con una regla la distancia que existe entre el extremo izquierdo de la escala hasta la marca asignada por el juez.